Discuss Scratch
- Discussion Forums
- » 日本語
- » Scratch数学カフェ
![[RSS Feed] [RSS Feed]](//cdn.scratch.mit.edu/scratchr2/static/__5b3e40ec58a840b41702360e9891321b__//djangobb_forum/img/feed-icon-small.png)
- kakurenbo
-
 Scratcher
Scratcher
500+ posts
Scratch数学カフェ
【問題】難易度:★★☆☆☆
その数が素数なら1を素数でなければ0を返す関数(出来れば数式)を作って下さい。
総和、三角関数の使用、中間処理の関数化等はOKですが、条件分岐、真偽値は使用不可です。
その式に至った経緯というか、説明をお願いしす。
想定解は用意してありますが、それと違っていても出来ていれば正解です。
その数が素数なら1を素数でなければ0を返す関数(出来れば数式)を作って下さい。
総和、三角関数の使用、中間処理の関数化等はOKですが、条件分岐、真偽値は使用不可です。
その式に至った経緯というか、説明をお願いしす。
想定解は用意してありますが、それと違っていても出来ていれば正解です。
Last edited by kakurenbo (Feb. 26, 2019 22:16:17)
- apple502j
-
 Scratcher
Scratcher
1000+ posts
Scratch数学カフェ
https://scratch.mit.edu/projects/289522150/
作りました。
nが素数かを調べるのには2-√nまでで割っていくと効率がいいです。
合成数だとわかったらすぐ終了します。
条件分岐は「()回繰り返す」に条件式を入れると回避できます。
作りました。
nが素数かを調べるのには2-√nまでで割っていくと効率がいいです。
合成数だとわかったらすぐ終了します。
条件分岐は「()回繰り返す」に条件式を入れると回避できます。
Last edited by apple502j (Feb. 26, 2019 12:07:10)
- kakurenbo
-
 Scratcher
Scratcher
500+ posts
Scratch数学カフェ
https://scratch.mit.edu/projects/289522150/すごいです!が、一応繰り返しはナシで…
作りました。
nが素数かを調べるのには2-√nまでで割っていくと効率がいいです。
合成数だとわかったらすぐ終了します。
条件分岐は「()回繰り返す」に条件式を入れると回避できます。
しかし、これはこれで美しいですね。
- ZeroX_Game
-
 Scratcher
Scratcher
100+ posts
Scratch数学カフェ
多分あってます!ちょっと問題とは違いますが速さから初速の角度を求める式をコメントとして記入しました(合ってるかなぁ)。
到達時間を固定した場合のサンプルを作ってみました。放物線
実装は厄介なのでしていません。
- ryorozyo
-
 Scratcher
Scratcher
1000+ posts
Scratch数学カフェ
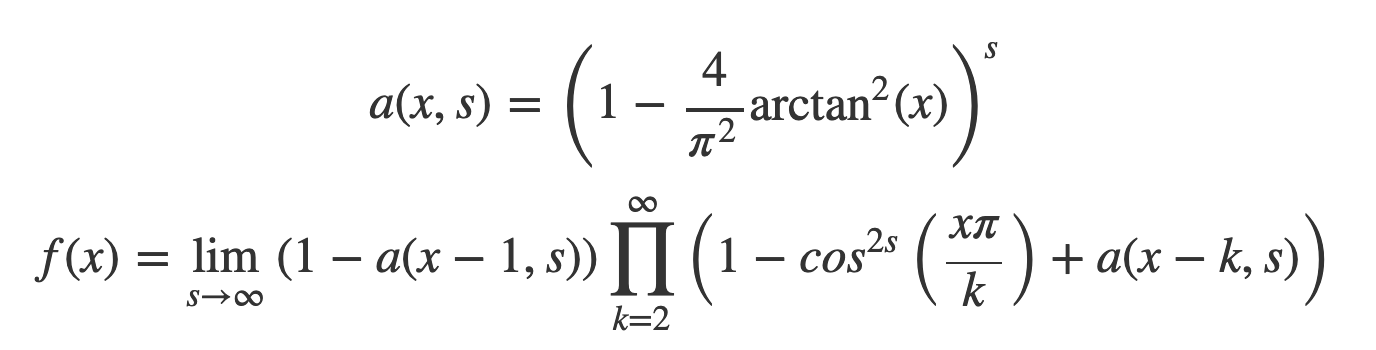
(なんかデカいけど)こんな感じですかね
(収束性とか考えてないけど多分収束するでしょう(解析学を雑にしかやってないので確かめるのがだるい人)
Last edited by ryorozyo (Feb. 27, 2019 01:34:43)
- kakurenbo
-
 Scratcher
Scratcher
500+ posts
Scratch数学カフェ
問題p(n)=n+p(n-1)*2+n
p(n)=n+p(n-1)*2+n
p(1)=1
p(10)=?
=2n+2p(n-1)
=2(n+p(n-1)),
p(1)=1
としてプログラムに組んでみました。解くのが面倒だっただけです。
定義 p(n)より、
もし <(n) = [1]> なら
[p-return v] を [1] にする
でなければ
p ((n) - (1))::costom
[p-return v] を (((n) + (p-return)) * (2)) にする
end
p(10) = 3560
であってますか?
Last edited by kakurenbo (April 4, 2019 06:46:12)
- watashida
-
 Scratcher
Scratcher
500+ posts
Scratch数学カフェ
問題一般項はp(n) = 3.5*2^n-2n-4 なので
p(n)=n+p(n-1)*2+n
p(1)=1
p(10)=?
p(10) = 3560
Last edited by watashida (April 4, 2019 06:49:34)
- hhayyatto
-
 Scratcher
Scratcher
1000+ posts
Scratch数学カフェ
正解問題一般項はp(n) = 3.5*2^n-2n-4 なので
p(n)=n+p(n-1)*2+n
p(1)=1
p(10)=?
p(10) = 3560
- choriss55
-
 Scratcher
Scratcher
100+ posts
Scratch数学カフェ
累乗根とかってどうやって計算すればいいんですか?
scratch上の累乗はわかります。ポケコン(PCG850VS)の累乗はn^(1/6)ってやれば⁶√n

scratch上の累乗はわかります。ポケコン(PCG850VS)の累乗はn^(1/6)ってやれば⁶√n
- になるけどscratchだとそれができないから、、、

- sky_77
-
 Scratcher
Scratcher
500+ posts
Scratch数学カフェ
累乗根とかってどうやって計算すればいいんですか?aのb乗は
((((a) の [ln v]::operators) * (b)) の [e^ v]::operators)で書けるので、aのb乗根は、
((((a) の [ln v]::operators) * ((1) / (b))) の [e^ v]::operators)でできます。(多少誤差があります。)
- ZeroX_Game
-
 Scratcher
Scratcher
100+ posts
Scratch数学カフェ
X^y乗は
被った上に僕の色おかしい
([e ^ v] \( (([In v] \( (x) \)) * (y)) \))でできるとabeeさんが前にどこかで書いてました。
被った上に僕の色おかしい
Last edited by ZeroX_Game (July 29, 2019 06:18:53)
- choriss55
-
 Scratcher
Scratcher
100+ posts
Scratch数学カフェ
ありがとうございます。累乗根とかってどうやって計算すればいいんですか?aのb乗は((((a) の [ln v]::operators) * (b)) の [e^ v]::operators)で書けるので、aのb乗根は、((((a) の [ln v]::operators) * ((1) / (b))) の [e^ v]::operators)でできます。(多少誤差があります。)
- Poteto143
-
 Scratcher
Scratcher
1000+ posts
Scratch数学カフェ
比例のグラフも、反比例のグラフも、xがただ一つに定まるとyもただ一つの値に定まることはわかりますよね。
それを利用して、スプライトのx座標を変化させながらその座標を式に代入して、y座標を求めれば良いのです。
ただ一つ、Scratchには面倒な仕様があり、
なので、
あ、ちなみに、このブロックだけではちゃんとしたグラフは作れません。
何が足りないのか、自分で判断してブロックを足して動くようにしてみて下さい
それを利用して、スプライトのx座標を変化させながらその座標を式に代入して、y座標を求めれば良いのです。
ただ一つ、Scratchには面倒な仕様があり、
ペンを下ろすの組み合わせではグラフが階段の形になってしまいます。
x座標を () ずつ変える
y座標を () にする
ペンを上げる
なので、
[x座標 v] を (1) ずつ変える // x座標という変数を作るという風にブロックを組む必要があります。わからなかったら聞いて下さい
x座標を ((x座標) + (x座標::variables)) 、y座標を ((x座標::variables) * (比例定数)) にする//比例のグラフの場合
あ、ちなみに、このブロックだけではちゃんとしたグラフは作れません。
何が足りないのか、自分で判断してブロックを足して動くようにしてみて下さい

- mary919
-
 Scratcher
Scratcher
16 posts
Scratch数学カフェ
比例のグラフも、反比例のグラフも、xがただ一つに定まるとyもただ一つの値に定まることはわかりますよね。わかりました!やってみます
それを利用して、スプライトのx座標を変化させながらその座標を式に代入して、y座標を求めれば良いのです。
ただ一つ、Scratchには面倒な仕様があり、ペンを下ろすの組み合わせではグラフが階段の形になってしまいます。
x座標を () ずつ変える
y座標を () にする
ペンを上げる
なので、[x座標 v] を (1) ずつ変える // x座標という変数を作るという風にブロックを組む必要があります。わからなかったら聞いて下さい
x座標を ((x座標) + (x座標::variables)) 、y座標を ((x座標::variables) * (比例定数)) にする//比例のグラフの場合
あ、ちなみに、このブロックだけではちゃんとしたグラフは作れません。
何が足りないのか、自分で判断してブロックを足して動くようにしてみて下さい
- Poteto143
-
 Scratcher
Scratcher
1000+ posts
Scratch数学カフェ
あ・・・一つ言い忘れたのですが、反比例のグラフを作るときで
((20) / (0))を実行すると「Infinity」という値を返します。これは「無限」という意味なのですが、数値として座標を決めるブロックに渡してしまうと0に移動してしまうので、条件分岐をうまく使って回避して下さい。
- ZeroX_Game
-
 Scratcher
Scratcher
100+ posts
Scratch数学カフェ
x,yと、x',y'を通る直線の式は
(x,y) = (t(x'-x),t(y'-y))
って表せるはず。こっちのほうがスクラッチでは扱いやすいかも。
(x,y) = (t(x'-x),t(y'-y))
って表せるはず。こっちのほうがスクラッチでは扱いやすいかも。