Discuss Scratch
- Discussion Forums
- » Suggestions
- » Could we please have an exponents block? ( ) ^ ( )
![[RSS Feed] [RSS Feed]](//cdn.scratch.mit.edu/scratchr2/static/__5b3e40ec58a840b41702360e9891321b__//djangobb_forum/img/feed-icon-small.png)
- _Paymer
-
 Scratcher
Scratcher
56 posts
Could we please have an exponents block? ( ) ^ ( )
12 years and this still has not been implemented.
- BZTC_Scratch
-
 Scratcher
Scratcher
74 posts
Could we please have an exponents block? ( ) ^ ( )
well, at least there's a workaround
- Lepus-Lacarotte
-
 Scratcher
Scratcher
84 posts
Could we please have an exponents block? ( ) ^ ( )
Since this conversation is completely unproductive, why are there still Scratchers wasting their time on it?
LL
LL
- jasonzawtun
-
 Scratcher
Scratcher
42 posts
Could we please have an exponents block? ( ) ^ ( )
Since this conversation is completely unproductive, why are there still Scratchers wasting their time on it?
LL
Dunno. Other than the exponent could be so useful that the Scratchers were begging to have it.
Last edited by jasonzawtun (Nov. 4, 2025 04:00:06)
- hotcrystal
-
 Scratcher
Scratcher
500+ posts
Could we please have an exponents block? ( ) ^ ( )
Since this conversation is completely unproductive, why are there still Scratchers wasting their time on it?Because people really want the exponent block to be in Scratch.
LL
- Toodchop
-
 Scratcher
Scratcher
100+ posts
Could we please have an exponents block? ( ) ^ ( )
Though if Scratch ever adds a bitwise XOR block in the future, the exponentiation block would probably use ** instead of ^, since ^ is usually used for bitwise XOR in most programming languages.There's a chance that it would look like this instead:I think it's more likeley to look like this:(() ** () :: operators)((2) ^ (5) ::operators)
- Steve0Greatness
-
 Scratcher
Scratcher
1000+ posts
Could we please have an exponents block? ( ) ^ ( )
Thought I'd just add to the discussion a little bit. Something commonly done for exponents in higher levels of math is to turn it into an exponent of e:

There are a few reasons why this is done, but one primary reason is that e is simply an extremely easy number to work with, especially in Calculus (for those who are wondering, it's because e^x is its own derivative). Anyway, Scratch provides functionality for both of these:
However, there is one major issue with this implementation: it cannot account for negative numbers. Scratch works exclusively within the real numbers, meaning it isn't able to work with the complex plane. This is an issue for one major reason: it makes accounting for negative numbers seemingly impossible. However, do not be fooled, as it still is, very much, possible.
Just for a quick explanation, of why it's important to be able to work with complex numbers, it's important to know about Euler's identity:

That “i” is sometimes called the “imaginary unit,” it's defined as the square root of -1.
This identity is important, as it allows for any negative number to be defined in terms of powers of e:

For example
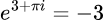
This can now be assumed to be part of the return value for the natural logarithm. Thus, the formula could be updated to:
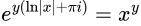
for when x < 0.
This can actually be split into 2 different exponents, which is what then makes it easier to solve:
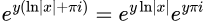
Notice how the left factor is, for non-negative numbers, equal to the number that it was before (as the absolute value returns the distance from 0 as a positive, real number); additionally, notice how the right factor only has one term that has i as a factor of it, which means it is able to be calculated using Euler's formula:
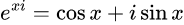
Substituting this in:
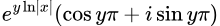
Since the cosine is the real part, it's the only part that we mostly care for.
There is also another part of this that needs to be taken care of before implementing it in Scratch: as Scratch uses degrees instead of radians, pi becomes 180.
The final thing that needs to be done now, is to make sure to only multiply by the cosine of y*180 if x < 0. This can be done fairly simply by multiplying the cosine operation by the boolean operator checking if x < 0, then adding that to 1.
You might notice a slight bit of inaccuracy, here, however, as far as I can tell, this inaccuracy is somewhat inherent to anything other than direct calculations of exponents. However, there is, indeed, a slight bit of other inaccuracy: there are certain cases where the returned number would output an imaginary number; in Scratch, as far as I can tell, the convention is to return NaN instead of 0, like this does. Meaning, a more accurate calculation might be:
However, as this uses 2 trig. functions, rather than just one, it is far more expensive (in terms of computation time) to run in Scratch.

There are a few reasons why this is done, but one primary reason is that e is simply an extremely easy number to work with, especially in Calculus (for those who are wondering, it's because e^x is its own derivative). Anyway, Scratch provides functionality for both of these:
([e ^ v] of ((y) * ([ln v] of (x)))::operators)
However, there is one major issue with this implementation: it cannot account for negative numbers. Scratch works exclusively within the real numbers, meaning it isn't able to work with the complex plane. This is an issue for one major reason: it makes accounting for negative numbers seemingly impossible. However, do not be fooled, as it still is, very much, possible.
Just for a quick explanation, of why it's important to be able to work with complex numbers, it's important to know about Euler's identity:

That “i” is sometimes called the “imaginary unit,” it's defined as the square root of -1.
This identity is important, as it allows for any negative number to be defined in terms of powers of e:

For example
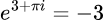
This can now be assumed to be part of the return value for the natural logarithm. Thus, the formula could be updated to:
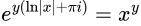
for when x < 0.
This can actually be split into 2 different exponents, which is what then makes it easier to solve:
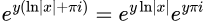
Notice how the left factor is, for non-negative numbers, equal to the number that it was before (as the absolute value returns the distance from 0 as a positive, real number); additionally, notice how the right factor only has one term that has i as a factor of it, which means it is able to be calculated using Euler's formula:
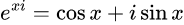
Substituting this in:
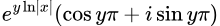
Since the cosine is the real part, it's the only part that we mostly care for.
There is also another part of this that needs to be taken care of before implementing it in Scratch: as Scratch uses degrees instead of radians, pi becomes 180.
(([e ^ v] of ((y) * ([ln v] of ([abs v] of (x))))::operators) * ([cos v] of ((y) * (180))))
The final thing that needs to be done now, is to make sure to only multiply by the cosine of y*180 if x < 0. This can be done fairly simply by multiplying the cosine operation by the boolean operator checking if x < 0, then adding that to 1.
(([e ^ v] of ((y) * ([ln v] of ([abs v] of (x))))::operators) * ((1) + ((2) * (<(x) < (0)> * ([cos v] of ((y) * (180)))))))
You might notice a slight bit of inaccuracy, here, however, as far as I can tell, this inaccuracy is somewhat inherent to anything other than direct calculations of exponents. However, there is, indeed, a slight bit of other inaccuracy: there are certain cases where the returned number would output an imaginary number; in Scratch, as far as I can tell, the convention is to return NaN instead of 0, like this does. Meaning, a more accurate calculation might be:
define (x) ^ (y)
set [absolute v] to ([e ^ v] of ((y) * ([ln v] of ([abs v] of (x))))::operators)
if <(x) < (0)> then
set [return v] to (absolute)
end
if <not <([sin v] of ((y) * (180))) = (0)>> then
set [return v] to [NaN]
end
set [return v] to ((absolute) * ([cos v] of ((y) * (180))))
However, as this uses 2 trig. functions, rather than just one, it is far more expensive (in terms of computation time) to run in Scratch.
- HollyEuca
-
 Scratcher
Scratcher
100+ posts
Could we please have an exponents block? ( ) ^ ( )
I hope an exponent block is added to 4.0 it'd be so useful!
((x) ^ (y))
- medians
-
 Scratcher
Scratcher
1000+ posts
Could we please have an exponents block? ( ) ^ ( )
Bringing this topic up.
I hope an exponent block is added to 4.0 it'd be so useful!I mean, you might want to elaborate((x) ^ (y))
Last edited by medians (Nov. 6, 2025 17:35:02)
- poppy849
-
 Scratcher
Scratcher
100+ posts
Could we please have an exponents block? ( ) ^ ( )
Bringing this topic up.Cool, I mean, there's no exponent block, nice suggestion! Suggesting them to elaborate, goodI hope an exponent block is added to 4.0 it'd be so useful!I mean, you might want to elaborate((x) ^ (y))
- HollyEuca
-
 Scratcher
Scratcher
100+ posts
Could we please have an exponents block? ( ) ^ ( )
Bringing this topic up.Well, I like making complicated math calculators/evaluators, but I can't make them do exponential math because there isn't an exponent block. And I don't believe it's possible to create an exponent block using pre-existing blocks that functions with all numbers, including negative numbers. It would simply be a little green block that would solve exponential math, presenting them either in standard or scientific notation, depending on the quantity.I hope an exponent block is added to 4.0 it'd be so useful!I mean, you might want to elaborate((x) ^ (y))
Here's an example of what it could do?
set [variable example v] to ((2) ^ (3))thanks
- hotcrystal
-
 Scratcher
Scratcher
500+ posts
Could we please have an exponents block? ( ) ^ ( )
Bumpie because dupe.
- wei04787
-
 Scratcher
Scratcher
100+ posts
Could we please have an exponents block? ( ) ^ ( )
+1
For people saying there is a work around, we know there is a work around but is really complicated for younger people and newer scratchers. Plus most blocks have a work around anyway.
For people saying there is a work around, we know there is a work around but is really complicated for younger people and newer scratchers. Plus most blocks have a work around anyway.
- Discussion Forums
- » Suggestions
-
» Could we please have an exponents block? ( ) ^ ( )
![[RSS Feed] [RSS Feed]](//cdn.scratch.mit.edu/scratchr2/static/__5b3e40ec58a840b41702360e9891321b__//djangobb_forum/img/feed-icon-small.png)











