Discuss Scratch
- Discussion Forums
- » 日本語
- » Scratchで競技プログラミング！(初めての人は最初の投稿をお読みください)
![[RSS Feed]](//cdn.scratch.mit.edu/scratchr2/static/__5b3e40ec58a840b41702360e9891321b__//djangobb_forum/img/feed-icon-small.png "[RSS Feed]")
![[RSS Feed]](http://cdn.scratch.mit.edu/scratchr2/static/__5b3e40ec58a840b41702360e9891321b__//djangobb_forum/img/feed-icon-small.png "[RSS Feed]"){kind=icon}
- sakura_neko
-
Scratcher
83 posts
Scratchで競技プログラミング！(初めての人は最初の投稿をお読みください)
#320 @Catapult-さん りんご拾い(Hard) 正解です!! FA!!
解答例はこちらです。
この問題は、移動可能な範囲のマスを「書いてある数字の小さい順」で探索することで解くことができます（りんごのマスは0とみなします）。
そこで、マスの位置と書いてある数字のペアを管理したいのですが、これをキューやスタックなどを使って直接管理すると小さいものを検索して取り出すのに最悪O(N²)かかってしまうのがネックです。そこで、追加と検索が高速にできるデータ構造として優先度付きキューを使うことを考えます。
優先度付きキューは平衡2分探索木を使って実装することもできますが、今回は「追加」と「最小値の削除」だけできればよいので、二分ヒープを使った実装で十分です。これはScratchでもそこまで複雑な実装を必要とせず、定数倍も軽いです。
このときそれぞれの操作は最悪でもO(logN)で行うことができます。
あとは最初のマスから始めて隣接するマスを優先度付きキューに入れて順番に取り出す操作を繰り返し、りんごのあるマスでは必ずりんごを拾いつつ最後のマスに辿り着けたかを判定すれば全体でO(N²logN)でこの問題を解くことができます。
この後でも他の人の実装例など受け付けてます！
解答例はこちらです。
この問題は、移動可能な範囲のマスを「書いてある数字の小さい順」で探索することで解くことができます（りんごのマスは0とみなします）。
そこで、マスの位置と書いてある数字のペアを管理したいのですが、これをキューやスタックなどを使って直接管理すると小さいものを検索して取り出すのに最悪O(N²)かかってしまうのがネックです。そこで、追加と検索が高速にできるデータ構造として優先度付きキューを使うことを考えます。
優先度付きキューは平衡2分探索木を使って実装することもできますが、今回は「追加」と「最小値の削除」だけできればよいので、二分ヒープを使った実装で十分です。これはScratchでもそこまで複雑な実装を必要とせず、定数倍も軽いです。
このときそれぞれの操作は最悪でもO(logN)で行うことができます。
あとは最初のマスから始めて隣接するマスを優先度付きキューに入れて順番に取り出す操作を繰り返し、りんごのあるマスでは必ずりんごを拾いつつ最後のマスに辿り着けたかを判定すれば全体でO(N²logN)でこの問題を解くことができます。
この後でも他の人の実装例など受け付けてます！
- Poteto143
-
Scratcher
1000+ posts
Scratchで競技プログラミング！(初めての人は最初の投稿をお読みください)
トピ主からのお知らせ
#1の説明文に、以下の通り変更を加えました！アレは嘘だ…ｹﾞﾌﾝｹﾞﾌﾝ
#1の説明文に、以下の通り変更を加えました！アレは嘘だ…ｹﾞﾌﾝｹﾞﾌﾝ
- 文章全体で、難しい言い回しやわかりにくい説明を直しました。
- 初心者向けにScratchスクリプトクイズトピックへ誘導する文章を追加しました。
- 設定できる実行時間制限を30秒までとするルールを撤廃しました。これはこのトピックを利用する皆さんのレベルがとても高くなっているのを鑑みて、もっと高難易度な問題を扱えるようにしたいという意図があります。ただし、どの問題にも必ず実行制限を設定しないといけないルールはこれまで通り変わりません。
- sakura_neko
-
Scratcher
83 posts
Scratchで競技プログラミング！(初めての人は最初の投稿をお読みください)
#323 @Doctor_Feさん りんご拾い(Easy, Hard) 正解です!! AC!!
なるほど、二分ヒープに追加する値の種類と個数が確定していることを利用して、分布数え上げソートの要領で二分ヒープをたかだかN²個のスタックに分解したんですね！これだと全体でもO(N²)で実際に想定解より高速なのでとてもいいと思います！
なるほど、二分ヒープに追加する値の種類と個数が確定していることを利用して、分布数え上げソートの要領で二分ヒープをたかだかN²個のスタックに分解したんですね！これだと全体でもO(N²)で実際に想定解より高速なのでとてもいいと思います！
- mikann-260
-
Scratcher
15 posts
Scratchで競技プログラミング！(初めての人は最初の投稿をお読みください)
問題一覧みたいなの作れませんか？
どんな問題があるかを一目でみられるようにしてほしいです。
どんな問題があるかを一目でみられるようにしてほしいです。
- Catapult-
-
Scratcher
100+ posts
Scratchで競技プログラミング！(初めての人は最初の投稿をお読みください)
水浸し 実行時間制限: 15秒
ある街にはN個の結節点とそれをつなぐM本の側溝からなる水路があります。
i番目の側溝(1≦i≦M)はai番目の結節点とbi番目の結節点を結び、長さはci[m]で表され、水は速さ1[m/s]で流れるものとします。
ある側溝から結節点に水が到達すると、結節点につながっている他の側溝にも水が流れ出します。
最初、水路のすべての結節点と側溝に水はないものとし、1番目の結節点に水を注いだとき、水路全体に水が広がるまでにかかる時間t[s]を出力してください。
制約
・入力
結節点の数N
側溝の本数M
各側溝の情報E=[a1, b1, c1, a2, b2, c2, …,aM, bM, cM]
ai, bj, cjは整数であり、1≦ai≦N、1≦bj≦N、1≦ci≦10³を満たすものとする(1≦i≦M)
(1≦i<j≦N)を満たすすべてのi, jにおいてi番目の結節点とj番目の結節点は側溝や結節点を介して繋がっているものとする(連結)
(1≦i<j≦M)を満たすすべてのi, jにおいてai≠bj, (ai,bi)≠(aj,bj)かつ(ai,bi)≠(bj,aj)が成り立つ(自己ループと多重辺を含まない)
Easy:2≦N≦100, 1≦M≦100、Hard: 2≦N≦1000, 1≦M≦10⁵
・出力
水路全体に水が広がるまでにかかる時間t
結果例
入力：N=4, M=5 E=[1,2,2,1,3,3,2,3,2,2,4,4,3,4,4]
出力：6.5
右図のようになります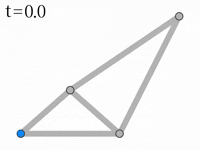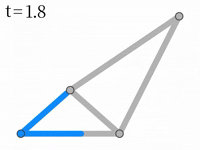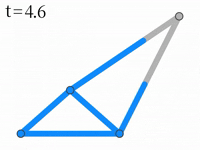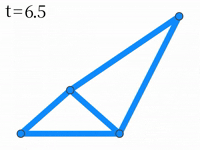
入力：N=5, M=7 E=[1,2,3,1,3,2,1,4,10,2,4,1,3,4,2,3,5,3,4,5,2]
出力：7
大きめのテストケース
追記: 2025/7/13 13:12 テストケースにミスがあったため変更しました
追記2: 2025/7/13 14:45 テストケースを再度変更しました
ある街にはN個の結節点とそれをつなぐM本の側溝からなる水路があります。
i番目の側溝(1≦i≦M)はai番目の結節点とbi番目の結節点を結び、長さはci[m]で表され、水は速さ1[m/s]で流れるものとします。
ある側溝から結節点に水が到達すると、結節点につながっている他の側溝にも水が流れ出します。
最初、水路のすべての結節点と側溝に水はないものとし、1番目の結節点に水を注いだとき、水路全体に水が広がるまでにかかる時間t[s]を出力してください。
制約
・入力
結節点の数N
側溝の本数M
各側溝の情報E=[a1, b1, c1, a2, b2, c2, …,aM, bM, cM]
ai, bj, cjは整数であり、1≦ai≦N、1≦bj≦N、1≦ci≦10³を満たすものとする(1≦i≦M)
(1≦i<j≦N)を満たすすべてのi, jにおいてi番目の結節点とj番目の結節点は側溝や結節点を介して繋がっているものとする(連結)
(1≦i<j≦M)を満たすすべてのi, jにおいてai≠bj, (ai,bi)≠(aj,bj)かつ(ai,bi)≠(bj,aj)が成り立つ(自己ループと多重辺を含まない)
Easy:2≦N≦100, 1≦M≦100、Hard: 2≦N≦1000, 1≦M≦10⁵
・出力
水路全体に水が広がるまでにかかる時間t
結果例
入力：N=4, M=5 E=[1,2,2,1,3,3,2,3,2,2,4,4,3,4,4]
出力：6.5
右図のようになります
入力：N=5, M=7 E=[1,2,3,1,3,2,1,4,10,2,4,1,3,4,2,3,5,3,4,5,2]
出力：7
大きめのテストケース
追記: 2025/7/13 13:12 テストケースにミスがあったため変更しました
追記2: 2025/7/13 14:45 テストケースを再度変更しました
Last edited by Catapult- (July 13, 2025 06:09:40)
- Catapult-
-
Scratcher
100+ posts
Scratchで競技プログラミング！(初めての人は最初の投稿をお読みください)
#331 @Nigi-Koro-chanさん 水浸し(Easy, Hard)正解です!! FA!!
データをリストに入力する前から計測しているにもかかわらず時間内に間に合っていて凄いです!!
解答例はこちらです。
この問題は言い換えると、「水路上のうち1番目の結節点からの最短距離が最長になるところまでの距離」を求めればよいとわかります。
そこで、考えやすくするためにまず各頂点までの最短距離を求めます。ここで、水路の重み付きグラフを隣接リスト表現で表し、ダイクストラ法を用いることでO((M+N)log(N))時間で済みます。
ダイクストラ法の実装には優先度付きキューを用いますが、これはリンゴ拾いの解答のようにバイナリヒープをリストで表現することで軽く実装できます。
あとは各辺に対して辺がすべて水で埋まるまでの時間を求め、それらの最大値をとることで答えとなります。この処理はO(M)時間です。ちなみに水路の途中で水が出会う場合にかかる時間は、i番目の辺の2頂点までの最短距離をそれぞれdist[ai], dist[bi]と表すと(dist[ai]+dist[bi]+ci)/2 で求められます(理由はぜひ考えてみてください)。
よって、全体としてはO((M+N)log(N))時間になります。(オーダー記法についてはあんまり自身がないので間違っているかもしれません)
初めての出題だったためテストケースの不備など迷惑もかけましたが、解いてもらって嬉しかったです。ありがとうございます！！
この後でも他の実装など受け付けてますのでどんどん回答してください!!
データをリストに入力する前から計測しているにもかかわらず時間内に間に合っていて凄いです!!
解答例はこちらです。
この問題は言い換えると、「水路上のうち1番目の結節点からの最短距離が最長になるところまでの距離」を求めればよいとわかります。
そこで、考えやすくするためにまず各頂点までの最短距離を求めます。ここで、水路の重み付きグラフを隣接リスト表現で表し、ダイクストラ法を用いることでO((M+N)log(N))時間で済みます。
ダイクストラ法の実装には優先度付きキューを用いますが、これはリンゴ拾いの解答のようにバイナリヒープをリストで表現することで軽く実装できます。
あとは各辺に対して辺がすべて水で埋まるまでの時間を求め、それらの最大値をとることで答えとなります。この処理はO(M)時間です。ちなみに水路の途中で水が出会う場合にかかる時間は、i番目の辺の2頂点までの最短距離をそれぞれdist[ai], dist[bi]と表すと(dist[ai]+dist[bi]+ci)/2 で求められます(理由はぜひ考えてみてください)。
よって、全体としてはO((M+N)log(N))時間になります。(オーダー記法についてはあんまり自身がないので間違っているかもしれません)
初めての出題だったためテストケースの不備など迷惑もかけましたが、解いてもらって嬉しかったです。ありがとうございます！！
この後でも他の実装など受け付けてますのでどんどん回答してください!!