Discuss Scratch
- Discussion Forums
- » 日本語
- » Scratchスクリプトクイズ
![[RSS Feed] [RSS Feed]](//cdn.scratch.mit.edu/scratchr2/static/__5b3e40ec58a840b41702360e9891321b__//djangobb_forum/img/feed-icon-small.png)
- inoking
-
 Scratcher
Scratcher
1000+ posts
Scratchスクリプトクイズ
作ってみました。もし端に着いたら、跳ね返ると同じ働きをするブロックを定義で作ってください。
比較用に「もし端についたら、跳ね返る」ブロックで動くものを同時に動かしています。
比較用に対し微妙にずれるのと
時々一か所でパタパタと止まってしまうのは勘弁してください。
もし端についたら、跳ね返る
- abee
-
 Scratcher
Scratcher
1000+ posts
Scratchスクリプトクイズ
そうですね。現状で作りうるのはこれが一番近いと思います。(私の回答例)
「もし端に着いたら、跳ね返る」は、反射(入射角と反射角を同じにする)こと以外に、スプライトが画面からはみ出ないようにすることを満たす必要があります。前者はできるのですが、後者はスプライトの大きさ(コスチュームの向きに応じてそれに外接する長方形)をスクリプトからリアルタイムで知る手段が用意されていないので、難しいと思います。
正解はGitHubのprimBounceOffEdge(とそれが呼び出している関数)にあります。私はSmalltalkerなので1.4のソースを読みました。
「もし端に着いたら、跳ね返る」は、反射(入射角と反射角を同じにする)こと以外に、スプライトが画面からはみ出ないようにすることを満たす必要があります。前者はできるのですが、後者はスプライトの大きさ(コスチュームの向きに応じてそれに外接する長方形)をスクリプトからリアルタイムで知る手段が用意されていないので、難しいと思います。
正解はGitHubのprimBounceOffEdge(とそれが呼び出している関数)にあります。私はSmalltalkerなので1.4のソースを読みました。
Last edited by abee (March 31, 2018 08:55:36)
- Nao_kun
-
 Scratcher
Scratcher
500+ posts
Scratchスクリプトクイズ
お題
LEVEL★☆☆☆☆((1) から (10) までの乱数)の代用ブロックを作る。
[どこか v] へ行くを使い、x座標またはy座標でうまく割って四捨五入でできると思います。
Last edited by Nao_kun (March 31, 2018 09:15:47)
- abee
-
 Scratcher
Scratcher
1000+ posts
Scratchスクリプトクイズ
[どこか v] へ行くというブロックはありません。
[ランダムな場所 v] へ行くだとすると、スプライトが動いてしまうので副作用が大きすぎます。
- hhayyatto
-
 Scratcher
Scratcher
1000+ posts
Scratchスクリプトクイズ
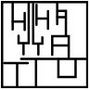
まじかお題
LEVEL★☆☆☆☆((1) から (10) までの乱数)の代用ブロックを作る。[どこか v] へ行くを使い、x座標またはy座標でうまく割って四捨五入でできると思います。
ちなみに自分の回答は
(すべて v) 番目を [乱数表 v] から削除するだと思っていた
[最小 v] を [1]にする
[最大 v] を [10] にする
<(最小) > (最大)> まで繰り返す
(最小) を [list v] に追加する
[最小 v] を (1) ずつ変える
end
((乱数 v) 番目( [乱数表 v] ) :: list) と言う
- abee
-
 Scratcher
Scratcher
1000+ posts
Scratchスクリプトクイズ
お題既出です。
LEVEL★☆☆☆☆((1) から (10) までの乱数)の代用ブロックを作る。
https://scratch.mit.edu/discuss/topic/133890/?page=19#post-2164038
- inoking
-
 Scratcher
Scratcher
1000+ posts
Scratchスクリプトクイズ
ベクトル演算方式にしたものを追加しました。作ってみました。もし端に着いたら、跳ね返ると同じ働きをするブロックを定義で作ってください。
比較用に「もし端についたら、跳ね返る」ブロックで動くものを同時に動かしています。
比較用に対し微妙にずれるのと
時々一か所でパタパタと止まってしまうのは勘弁してください。
もし端についたら、跳ね返る
ベクトル演算方式にすると反射はベクトル成分を反転するだけで済みますが
スプライトの「向き」は
真上が0度、時計回りが+方向、反時計回りが-方向というヘンテコな?座標系になっているため
一般的な
右が0度、反時計回りが+方向、時計回りが-方向という座標系との変換が必要です。
また、
時々一か所でパタパタと止まってしまうのを対策しました(苦しまぎれですが)。
- egunattu
-
 Scratcher
Scratcher
63 posts
Scratchスクリプトクイズ
まじかお題
LEVEL★☆☆☆☆((1) から (10) までの乱数)の代用ブロックを作る。[どこか v] へ行くを使い、x座標またはy座標でうまく割って四捨五入でできると思います。
ちなみに自分の回答は(すべて v) 番目を [乱数表 v] から削除するだと思っていた
[最小 v] を [1]にする
[最大 v] を [10] にする
<(最小) > (最大)> まで繰り返す
(最小) を [list v] に追加する
[最小 v] を (1) ずつ変える
end
((乱数 v) 番目( [乱数表 v] ) :: list) と言う
定義 (はじめ)から(おわり)おわりまでの乱数
[数 v] を (はじめ) にする
(おわり) 回繰り返す
(数) を [データ v] に追加する
[数 v] を (1) ずつ変える
end
[結果 v] を ((乱数 v) 番目( [データ v] ) :: list) にする
- Nao_kun
-
 Scratcher
Scratcher
500+ posts
Scratchスクリプトクイズ
いろいろすみません。[どこか v] へ行くというブロックはありません。[ランダムな場所 v] へ行くだとすると、スプライトが動いてしまうので副作用が大きすぎます。
- dream1030
-
 Scratcher
Scratcher
500+ posts
Scratchスクリプトクイズ
ハッキングですね。定義 ペンの色を[#ffffff]にする(ペンの色を [#50f07f] にするの代用ブロック教えて)
Scratch2.0をハッキングしよう!
Scratch 2.0をハッキングしよう! 続
へどうぞ。
追記:語尾が質問っぽかったので質問コーナーみたいに回答してしまいましたが…クイズでしたか?
Last edited by dream1030 (April 27, 2018 23:52:08)
- watashida
-
 Scratcher
Scratcher
500+ posts
Scratchスクリプトクイズ
https://scratch.mit.edu/projects/219375471/定義 ペンの色を[#ffffff]にする
(ペンの色を [#50f07f] にするの代用ブロック教えて)
こんな感じで
ペンの色を[#50f07f]にするを使わず書くことはできた
- punpunta
-
 Scratcher
Scratcher
8 posts
Scratchスクリプトクイズ
お題★★★★★★★★(できないかも。)(クイズにならねえ)
[すべて] を止めるの力を、全スプリクトの力で打ち破れ!
Last edited by punpunta (May 14, 2018 12:01:51)
- GANDAM5
-
 Scratcher
Scratcher
100+ posts
Scratchスクリプトクイズ
お題★☆☆☆☆☆☆☆☆(できないかも。)(クイズにならねえ)[すべて] を止めるの力を、全スプリクトの力で打ち破れ!
[ タイマーv] > (0) のとき
ずっと
タイマーをリセット
end
このスプライトがクリックされたとき
[すべて v] を止める
Last edited by GANDAM5 (May 14, 2018 19:33:24)
- fine316
-
 Scratcher
Scratcher
1000+ posts
Scratchスクリプトクイズ
<((1) から ((11) から (20) までの乱数) までの乱数) = [1]>がtrueとなる確率を求めよ。
- ARATAKU
-
 Scratcher
Scratcher
500+ posts
Scratchスクリプトクイズ
1/(11+8*9/2)とは言いましたが、実際にやってみたら、別の結果になりました。(あえてやってみた結果は言いませんが。)
で、
1/47(1分の47)になると思う。
- tyawanmusi
-
 Scratcher
Scratcher
100+ posts
Scratchスクリプトクイズ
さよなら500キリ番・・・
そのうち乱数が1になるのは10パターンだから、
10/155=2/31より、2/31になる・・・はず
パターン数は11+12+13+~+18+19+20より、155。<((1) から ((11) から (20) までの乱数) までの乱数) = [1]>がtrueとなる確率を求めよ。
そのうち乱数が1になるのは10パターンだから、
10/155=2/31より、2/31になる・・・はず
Last edited by tyawanmusi (May 15, 2018 07:57:43)